El primer ejemplo de átomo artificial que quiero presentar en este monográfico es, por contra, el que menos conozco, ya que no he trabajado nunca con ellos. Solo tengo el gusto de haberlos conocido en congresos generalistas. Para ello antes tengo que hablar sobre el concepto de superconductividad. La idea básica de un superconductor reside en que a temperaturas suficientemente bajas los electrones en el seno de ciertos metales dejan de comportarse como unidades individuales. Un metal está formado por una red periódica y simétrica de átomos organizados entre ellos. En concreto esa red se compone por iones positivos localizados y un conjunto de electrones compartidos por toda la red. Aquí conviene pararse un momento. Aunque esa estructura cristalina contiene iones positivos y electrones, para poder describir el sistema se suele usar una ficción. En lugar de estudiar los electrones por separado, usando su naturaleza fundamental descrita por el modelo estándar del que hablé en el quinto nivel de esta serie, los electrones en un cristal normalmente se estudian usando una naturaleza distinta. Usualmente a la naturaleza del electrón se le añade la interacción con la red cristalina. Digamos que hablamos de “electrones efectivos”. Estos electrones efectivos son un ejemplo de lo que se denomina cuasipartículas. Entes que copian el nombre de los elementos del modelo estándar que presentaba en el quinto nivel, aunque añaden ese prefijo “cuasi” para advertir de que algo raro sucede. Son entidades cuasi-fantasmagóricas, que, por ejemplo, nos ayudan a entender el comportamiento de los electrones en el seno de un cristal, como sucede en el caso de un metal. En ese metal superconductor, los electrones efectivos compartidos entre el mallado de iones positivos, al moverse por la red pueden interaccionar con los propios iones positivos, ya que, como sabemos, las cargas eléctricas opuestas se atraen. Cuando la temperatura es lo suficientemente baja, en determinados materiales como el mercurio, el aluminio, o el estaño, o en otros materiales más complejos como el diboruro de magnesio, dos electrones pueden vencer su fuerza de repulsión mutua al ser atraídos por la fuerza positiva de un ion. Pero la casuística es más complicada. En concreto, ese ion no es un ion localizado, sino una vibración material de la propia estructura cristalina, como lo es el propio sonido. Ese tipo de vibración de los iones se propaga por la red cristalina, y de hecho constituye otra nueva cuasipartícula, llamada fonón. La propagación del par enlazado de electrones junto esa vibración del ion positivo, o fonón, se produce sin resistencia eléctrica. En términos macroscópicos se produce una corriente que no posee una resistencia a su propagación. Bajo el contexto de la física de superconductores podríamos decir que, efectivamente, 1+1 es distinto de 2. El par de electrones enlazados se ha llamado par de Cooper. Y, sí, el par de Cooper también es otra cuasipartícula.

Los pares de Cooper son cuasipartículas formadas por parejas de electrones que dan origen al fenómeno de la superconductividad.
Con esto podríamos “cuasi-entender” el fenómeno de la superconductividad. O al menos podríamos entrever los mecanismos que hacen que en estos materiales cristalinos aparezca una nueva naturaleza pseudo-real, cuasi-natural, asociada a la interacción y la propagación de cuasipartículas. Pero para hablar de átomos artificiales tenemos que dar un salto tecnológico. Desde este punto de vista tecnológico, cuando se consigue unir dos materiales superconductores entre otro material no superconductor se puede construir lo que viene llamándose una unión de Josephson. Un voltaje entre los dos superconductores puede generar una corriente túnel de pares de Cooper que atraviese el material no superconductor. Y lo que es más importante, la corriente que se genera no sigue la ley de ohm, una relación entre corriente y potencial eléctrico lineal. Este tipo de uniones de Josephson se pueden incluir en circuitos eléctricos convencionales.
Antes de seguir el camino hasta nuestro primer átomo artificial, detengámonos levemente sobre alguna característica sencilla de los circuitos convencionales. En electrónica elemental, el sistema compuesto por un inductor-L (o bobina, que podemos entenderla como un almacén de energía en forma de campo magnético, que puede ser devuelta al circuito al sufrir cambios de corriente) y un condensador-C (que podemos entender como un almacén de energía mecánica que puede devolverse en forma carga y descarga de corriente), se conoce como circuito LC. Cuando este circuito se alimenta con una corriente alterna a la frecuencia de resonancia, el circuito reproduce un modelo de oscilador armónico simple (un muelle es un ejemplo de oscilador armónico, donde la energía potencial se transfiere a energía cinética, y viceversa, de forma periódica). El diagrama energético de un oscilador armónico simple se puede formalizar matemáticamente como un conjunto de niveles energéticos equiespaciados. O lo que es lo mismo, un sistema lineal donde la energía del estado será un múltiplo del número de elementos del estado. Pasa exactamente lo mismo con la energía del campo electromagnético. Como sabemos, la luz es una onda electromagnética, que viene descrita por un movimiento armónico. A su vez la luz puede describirse desde su formulación fotónica. O lo que es lo mismo, por fotones. Partículas con una energía discreta. La energía total de este sistema, al ser lineal, será múltiplo del número de fotones. Por ejemplo, el estado de tres fotones tendrá tres veces más energía que el estado de un fotón. Este tipo de comportamiento se puede modelizar usando los circuitos LC. Volvamos ahora a las uniones Josephson.
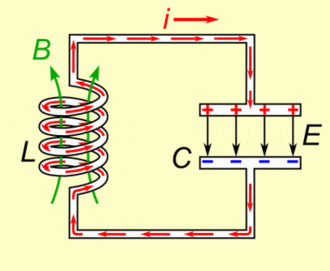
Diagrama básico de un circuito LC.
Si en este sistema básico compuesto por inductor más condensador sustituimos al inductor por una unión Josephson, el resultado es que, debido a la no linealidad de la relación de corriente frente al potencial de la unión superconductora, el oscilador deja de comportarse armónicamente para comportarse como un oscilador anarmónico. O lo que es lo mismo, un oscilador con una respuesta no lineal. En este caso, el estado de n componentes no tendrá una energía total igual a n por la energía de cada componente. Da la casualidad de que este tipo de potencial no lineal es precisamente el que siguen los propios átomos. Por tanto, con estos circuitos con elementos superconductores se podría simular el propio potencial de un átomo natural. En otras palabras, estos circuitos se pueden considerar como átomos artificiales. Con una gran ventaja, ya que estos átomos artificiales pueden ser incluidos dentro de otros circuitos electrónicos, que permiten manipularlos, localizarlos y controlarlos de forma mucho más precisa y sencilla. Por ejemplo, bajo estas estrategias actualmente se están diseñando cristales atómicos, o redes atómicas, … artificiales, por supuesto. Algunas de estas propuestas pretender ser la base para el desarrollo tecnológico de la computación cuántica.


 No hay comentarios
No hay comentarios









